Avendo intenzione di procedere ad un'analisi balistica dei miei fucili con telecamera ad alta velocità ( ma a cosa mi servirà mai, Vi chiederete ), mi sono chiesto quali possano essere i pregi ed i limiti dell'uso di una simile metodica nello studio della velocità dell'asta sia durante la fase di balistica interna che durante quella di balistica esterna.

La domanda che mi sono posto è stata sostanzialmente la seguente: dovendo procedere eventualmente all'acquisto di un'apparecchiatura non proprio economica, quali possono essere i risultati che essa mi può fornire?
Le sorprese non sono mancate.
Il mercato delle telecamere digitali a rapida acquisizione di immagini è un mercato che è risulato essere, con mia grande sorpresa, molto ampio e caratterizzato da modelli con ampie variazioni di caratteristiche e soprattutto prezzo ( si va da qualche migliaio di Euro a diverse decine di migliaia di Euro, a prezzi "sconosciuti").
Mi sono soffermato su un modello medio con un frame rate di 1000 acquisizioni reali al secondo ed una risoluzione di 720 pixel in larghezza, senza sforare in modelli ben oltre le me intenzioni di studio ( vale a dire telecamere "tipo" Full HD con velocità di aquisizione di diverse decine di migliaia di immagini al secondo).
Partendo da tali presupposti la mia attenzione, dunque, è ricaduta sulla tipologia di telecamere appena descritta ipotizzando un modello di studio.
Tale modello prevede la possibilità di effettuare riprese a "tutto campo" comprendente cioè sia la fase di balistica interna che esterna, al fine dell'elaborazione di una curva velocità/spazio, spazio/tempo percorso lungo la gittata utile.
Mi sono reso conto che tale ripresa deve essere necessariamente dell'ordine di circa 6 metri di campo, ossia la telecamera deve poter inquadrare la distanza più ravvicinata possibile, al fine di avere la minima perdita di informazioni dovute alla risoluzione stessa della telecamera, alla scena che mi interessa filmare.
Non bisogna infatti dimenticare che l'immagine della telecamera è elaborata grazie ad una "rete" di pixel ( puntini luminosi ) la cui "accensione" consente di costruire "frame dopo frame" le riprese filmate.
Ad ogni pixel può essere fatta corripondere una determinata distanza "reale" a seconda della larghezza del campo di ripresa e della risoluzione della telecamera. In effetti sarebbe più opportuno parlare di "superfici" e non segmenti in quanto ad ogni pixel corrisponde una superficie. Ma essendo l'analisi che mi interessa sostanzialmente "monodimensionale" (ossia una distanza in funzione del tempo) possiamo riferirci al pixel in senso di larghezza trascurando altri aspetti come la forma del pixel, il PAR (Pixel aspect ratio) o l'IAR ( Image aspect ratio) che complicherebbero solo la trattazione senza aggiungere informazioni utili.
Immaginando un campo di ripresa di 6 metri, dunque, avremo che un pixel di una telecamera a 720 pixel copre un segmento reale di circa 0,83 cm ( 600 cm / 720 pixel), mentre per un campo di ripresa più ravvicinato di 1,5 metri ( come può essere per la balistica interna ) avremo che un pixel corrisponde ad una distanza reale di circa 0,21 cm (150 cm / 720 pixel ).
E' logico che le dimensioni di un "segmento reale" riprese da un pixel sono inversamente proporzionali alla risoluzione video (al crescere della risoluzione diminuisce il segmento reale coperto dalla telecamera) e direttamente proporzionale alla larghezza del "campo di visione" (al crescere del campo di visione cresce il segemento reale coperto da ogni singolo pixel).
Le due immagini che seguono chiariscono meglio il concetto:

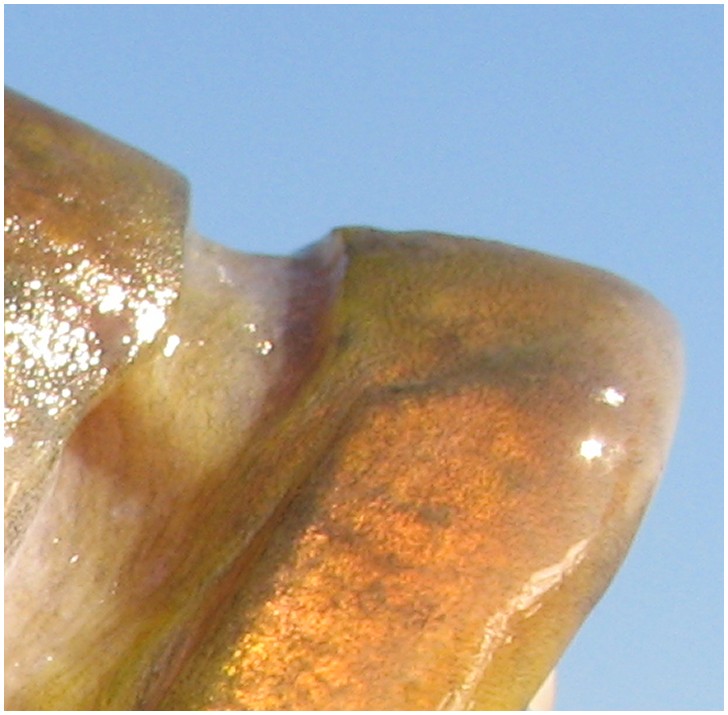
Sono entrambe delle immagini alla risoluzioni di 720 pixel (clicca sull'immagine) di larghezza ottenute da un'unica foto a risoluzione maggiore. E' come aver fotografato lo stesso soggetto (la bocca di un bel dentice) a due diverse distanze.
Zoomando fino ad ottenere la possibilità di visione dei singoli pixel avremo, nell'immagine scattata a maggiore distanza, una visione più sgranata poichè ogni pixel "copre" una distanza reale maggiore, mentre nell'immagine a minore distanza avremo una maggiore omogeneità perchè ogni singolo pixel copre distanze ( in realtà come dicevo prima "superfici") più piccole.

Ma come si traduce tutto questo nell'analisi balistica?
Volendo riprendere nel mio modello ipotetico una scena di balistica interna + balistica esterna (cioè una larghezza minima che ci consenta di inquadrare fucile + gittata dell'asta ) avremo bisogno di una scena di inquadratura larga circa 6 metri.
A queste condizioni, con una telecamera a 1000 fps e risoluzione di 720 pixel, avremo che un ogni pixel copre, come dicevo, la distanza reale di 0,83 cm, ossia quasi un centimetro .
In sostanza per ricostruire la curva velocità/spazio di un'asta con una telecamera ad alta velocità avremmo a disposizione due parametri da analizzare:
- lo spazio, rappresentato dai singoli pixel "accesi" durante lo spostamento dell'asta
- il tempo, rappresentato dal frame rate.
Nel caso della telecamera supposta lo spazio è di 0,83 cm a pixel, il tempo è rappresentato dal frame rate ossia 1000 fps (ossia 1000 millisecondi).
Ma come sfruttare queste informazioni e soprattutto quali sono i loro limiti?
Sappiamo che un tiro medio ( dove per tiro medio intendo il tiro medio espresso da un fucile, non la media dei tiri; in effetti i cultori di statistica parlerebbero di "moda" e non di "media", ma fatemi passare l'imprecisione linguistico-statistica) ha una Velocità di picco di circa 28 m/sec ed una velocità residua, a 4 metri senza sagola, di circa 16 m/sec (logicamente tali valori sono solo indicativi subendo ampie oscillazioni a secondo del fucile, asta, elastici etc usati. Io li userò solo come punto di riferimento per la mia analisi sull'uso della telecamera ad alta velocità).
Come "vede" la telecamera un oggetto posto in un'inquadratura di 6 metri e che si muove a 28 m/sec o a 16 m/sec ?
Analizziamo dapprima il caso dell'oggetto che si muove a velocità di 28 m/sec (supponiamo che la velocità sia costante solo per non complicare ulteriormente le cose) su uno sfondo fisso ed immobile.
Un oggetto che si muove a tale velocità compie un percorso di 2,8 cm/msec (2800 cm / 1000 msec).
Ossia ( poichè ogni frame dura 1 msec ) vi è uno spostamente di 2,8 cm tra il frama A ed il frame B ( immediatamente successivo ad A ).
In termini di pixel avremo che tra il frame A ed il frame B si sono accessi:
2,8 / 0,83 = 3,37 pixel
Qui abbiamo un primo problema: il pixel conosce in sostanza, nel modello da noi ipotizzato, solo due stati: o rimane immodificato ( significando che l'oggetto in movimento, ossia l'asta, non è entrato nella sua "superficie" di ripresa) o si modifica ( diciamo impropriamente che si "accende") poichè l'oggetto che ci interessa è entrato nella sua superficie di competenza.
In pratica ai fini della nostra analisi possiamo considerare un pixel una sorta di bit ( elemento binario): acceso o spento, 1 o 0.
Ma come considerare quella porzione di 0,37 pixel che corrisponde al limite di lettura della nostra ipotetica telecamera ? Acceso o spento?
Ossia l'oggetto che si muove a 28 m/sec nella situazione di campo di ripresa ipotizzato ( 6 metri) con la telecameta ipotizzata ( 1000 fps, 720 pixel di copertura), "accende" 3 o 4 pixel ?
Se accende 3 pixel avremo che, per un oggetto che si muove a 28 m/sec, calcoleremo una velocità media di :
0,8333 ( lo spazio in cm coperto da un pixel) X 3 ( il numero di pixel accesi) / 1 frame (msec) = 2,49 cm/msec ossia 24,9 m/sec
Nel secondo caso ( 4 pixel accesi) avremo una velocità media di :
0,83 cm* 4 / 1 msec = 3,32 cm/msec = 33,2 m/sec
In pratica nel primo caso abbiamo abbiamo ampiamente sottostimato la velocità di 28 – 24,9 = 3,1 m/sec
Nel secondo caso l'abbiamo ampiamente sovrastimata di 33,2 -28 = 5,2 m/sec con un range di 8,30 m/sec.
Tale valore di approssimazione è logicamente inaccettabile per un'analisi corretta.
Ma come poter migliorare le cose con le acquisizioni a nostra disposizione?
Poichè l'intervallo di tempo misurabile è fisso (ossia il frame rate della telecamera), ciò che possiamo fare, al fine di ridurre l'approssimazione, è aumentare lo spazio misurato (ossia misurare la distanza non per frame successivi, ma saltando un certo numero di frame cui corrisponde un maggior percorso dell'oggetto che stiamo studiando).
Vediamo cosa succede per spazi (ossia intervalli di frames) via via crescenti. La situazione è riassunta nella seguente tabella:
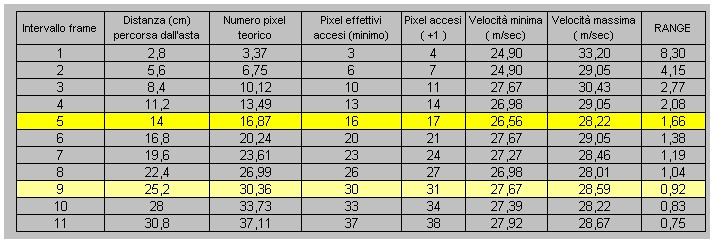
E' da notare che al diminuire del range di approssimazione, aumenta l'intervallo di frames e quindi il numero di pixel "accesi" ( la distanza percorsa dall'asta è maggiore). In altri termini, man mano che il range di approssimazione diminuisce, calcoliamo una velocità MEDIA per tratti sempre più ampi.
A prima analisi potrebbe essere scelto come "break point" un range inferiore a 2 m/sec o a 1 m/sec, cui corriponde il calcolo della velocità MEDIA su un tratto rispettivamente di circa 14 cm e 25 cm.
Per velocità inferiori ( ad esempio 16 m/sec ), a parità di intervallo di numero di frames, avremo una distanza percorsa inferiore e, quindi, la precisione della metodica tende logicamente ad aumentare per uguali intervalli di spazio. Ad esempio, come si può desumere dalla tabella seguente, ad un intervallo di circa 25,6 cm (alla velocità di 16 m/sec) corrisponde un range di 0,52 m/sec, mentre (alla velocità di 28 m/sec) ad un intervallo di 25,2 cm corrisponde un range quasi doppio (0,92 m/sec).
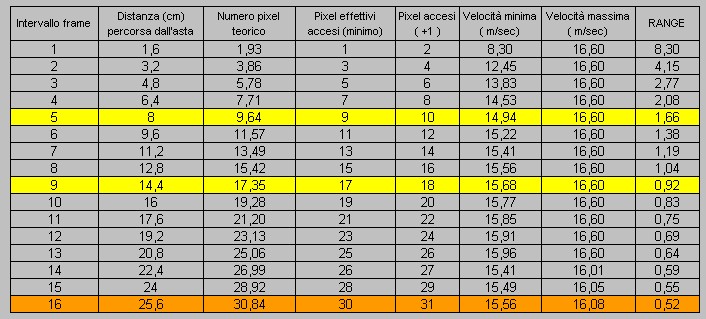
Riflessioni.
L'uso della telecamera ad alta velocità per lo studio balistico di un fucile subacqueo è sicuramente una metodica eccellente in quanto riesce a raccogliere informazioni che l'occhio umano non riesce a percepire. Pur tuttavia (almeno per i modelli economicamente abbordarbili ed al di fuori di un uso altamente professionale), soffre di un potenziale grado di approssimazione nel fornire i dati necessari a costruire i grafici spazio/velocità e spazio/tempo. A ciò si aggiunge una lenta acquisizione dei dati , poichè è necessario extrapolare gli stessi "frame by frame" (almenocchè non venga sviluppato un qualche software d'analisi grafica specifico).
Un promettente vantaggio di tali apparecchiature sembra comunque essere il progressivo decrescere dei prezzi, che nell'arco di qualche lustro si porteranno verosimilmente su valori di tipo "consumer". E' interessante notare, ad esempio, che solo da due-tre anni inizi a "circolare" sul web qualche prezzo relativo a tali apparecchiature. Prima di allora era perfino difficile reperire tali dati. Probabilmente i documentari tipo "Slow Motion" hanno dato un notevole impulso al settore.
Nell'attesa, i dati relativi allo studio balistico delle velocità possono essere ricavati con metodiche alternative, sicuramente più economiche e, se ben congeniate, più precise rispetto ai modelli di telecamere attualmente "abbordabili" poichè in grado di analizzare intervalli di spazio inferiori ai 10 cm ed intervalli di tempo con approssimazione inferiore al ½ msec.
Tali metodiche saranno oggetto di future investigazioni.
PS: Qualsiasi opinione, osservazione, correzione, rettifica in merito al presente articolo è ben accetta e sarà aggiunta, qualora l'Autore lo desideri, in calce indicandone eventualmente la fonte.
A seguire qualche link da dove iniziare ad esplorare il mondo "High Speed Cam":
- http://en.wikipedia.org/wiki/High_speed_camera
- http://www.mikrotron.de/index.php?en_hsv_kamerabegriffe
- http://www.visionresearch.com/
- http://createdigitalmotion.com/2006/08/30/high-speed-camera-rental-prices-for-the-people/
- http://www.lot-oriel.com/site/pages_it_it/products/highspeed_cameras/highspeed_cameras.php